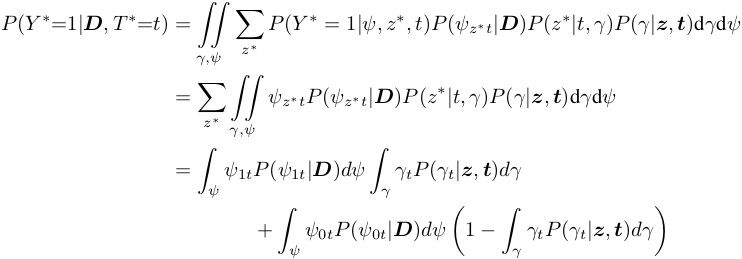In this post we explain a Bayesian approach to inferring the impact of interventions or actions. We show that representing causality within a standard Bayesian approach softens the boundary between tractable and impossible queries and opens up potential new approaches to causal inference. This post is a detailed but informal presentation of our Arxiv papers: Replacing the do calculus with Bayes rule, and Causal inference with Bayes rule — also see our video presentation Bayesian Causality.
Causality — what it is and how to infer it — has been one of the most controversial subjects of machine learning and statistics. The recent publication of the Book of Why has re-ignited a long running debate on whether causal inference can be done within the standard Bayesian modelling paradigm or if it requires a fundamentally different approach. This debate began between Pearl and Rubin in the 90’s and continues today — particularly on Andrew Gelman’s blog — see Gelman and Pearl. In this post we discuss some of our recent work that aims to bridge this debate.
Read the full blog post on Medium.